Self attention

2024/08/15
Karpathy Self attention Transformers

Overview

This is my notes after watching Karpathy's Let's build GPT: from scratch, in code, spelled out.lecture. A while ago, when I looked at images like the following that try to explain how a token has more attention to other tokens, I could not quite follow. after watching this video, and executing the code, I think, I am better now.

When I was reading docs about attention, and transformers, I had many doubts:

Given a sentence, how does a word/token know to give high attention to specific words?
How Query, Key, and Value matrices are used in attention?
What exactly is attention?

Did this lecture answer all my questions? I don't know, but, I am at least better than before.

./images/visualize-attention.png

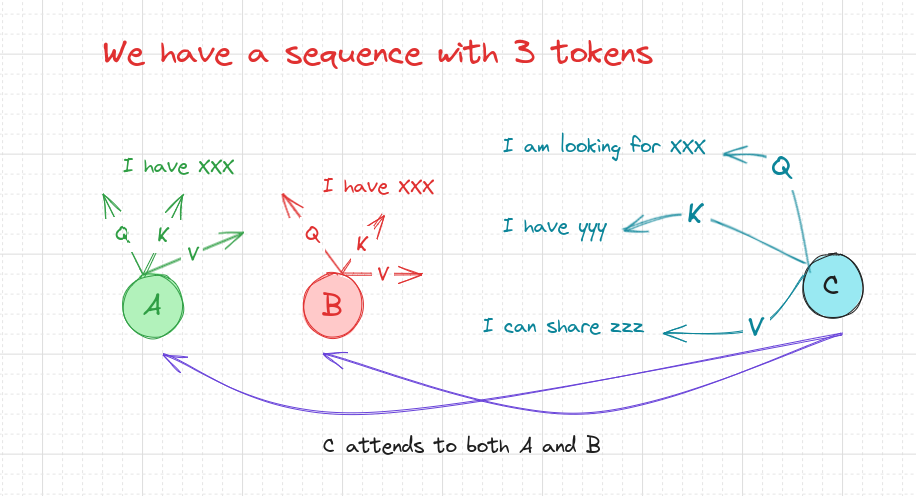
Query, Key, and Value matrices

Each token in the sequence has its own query, key, and value vectors.

./images/self-attention-overview.png

Help from Claude

import torch  
from torch.nn import functional as F  
import torch.nn as nn  
  
torch.manual_seed(1337)  
  
B, T, C = 4, 3, 5  # batch, time, channels  
x = torch.randn(B, T, C)  
  
head_size = 6  
  
# What am i looking for?  
query = nn.Linear(in_features=C, out_features=head_size, bias=False)  
  
# What do I have ?  
key = nn.Linear(in_features=C, out_features=head_size, bias=False)  
  
# What I can share?  
value = nn.Linear(in_features=C, out_features=head_size, bias=False)  
  
k = key(x)  
q = query(x)  
v = value(x)  
  
wei = q @ k.transpose(-2, -1) * head_size**-0.5   # Scaled dot product  
  
tril = torch.tril(torch.ones(T, T))  
wei = wei.masked_fill(tril == 0, float('-inf'))  
wei = F.softmax(wei, dim=-1)  
out = wei @ v

I asked Claude to explain this code to a kid, and this is how it responded:

Alright, let's try to explain this in a simpler way, imagining we're talking about a classroom of kids:

First, we have a classroom (our input x). There are 4 groups of kids (B=4), each group has 3 kids (T=3), and each kid knows 5 things about themselves (C=5).
Now, we want to play a game where each kid learns from the others, but they can only learn from the kids who came before them in line.
We give each kid three special tools:
1. A "what I'm looking for" tool (query)
2. A "what I have" tool (key)
3. A "what I can share" tool (value)
Each kid uses these tools to change their 5 things into 6 new things (head_size=6).
Then, each kid does this:
1. They use their "what I'm looking for" to check how well it matches with everyone's "what I have".
2. This is like each kid asking, "Do you have what I'm looking for?"
But remember, they can only ask kids who came before them in line. So we cover up the answers from kids who come after (that's the tril and masked_fill part).
Then, each kid decides how much attention to pay to each of the kids before them. They can't pay attention to kids after them (that would be cheating!).
Finally, each kid learns new things based on how much attention they paid to each kid before them. They mix together the "what I can share" information from the other kids, giving more importance to the kids they paid more attention to.
The result (out) is what each kid learned from this game, based on what they were looking for and what the other kids before them could share.

This game helps each kid learn things that are most relevant to what they're looking for, but only from the kids who came before them in line. It's a way of mixing and matching information in a smart way!

How Value matrix is useful?

Since explanation is for the code snippet above.

The v matrix ("value" matrix) represents the actual information or content from each position that we want to gather or aggregate. When we do wei @ v, we're essentially doing a weighted sum of the values, where the weights are determined by our attention mechanism.

Here's why we need the v matrix:

**Information content:

While q (query) and k (key) are used to calculate "where" to pay attention, they don't contain the actual information we want to gather. v contains the information we actually want to aggregate.

Separation of concerns:

By separating "what to attend to" (determined by q and k) from "what information to gather" (v), we give the model more flexibility. This allows the model to potentially attend to one aspect of the input while retrieving related but different information.

Analogy:

Imagine you're at a big party (your input sequence).
q is like you asking "Who knows about cooking?" (your query)
k is like each person's expertise (their keys)
wei (after softmax) is like you figuring out who to listen to about cooking
v is the actual cooking tips each person has
wei @ v is like you gathering cooking tips, paying more attention to the people you determined know more about cooking

Without v, we would only know where to pay attention, but we wouldn't have any information to gather from those attention points. The v matrix gives us the actual content to aggregate based on our calculated attention weights.